Cryptography
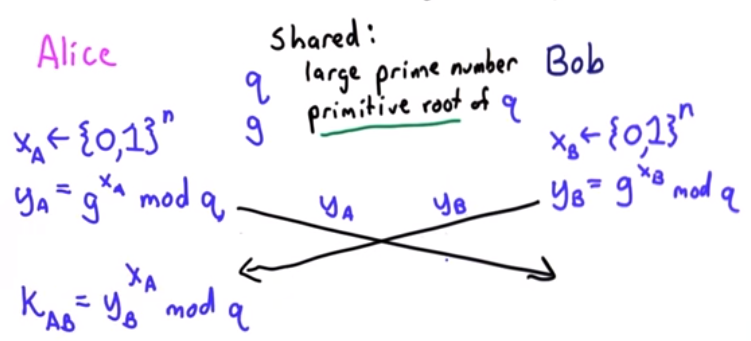
Diffie-Hellman key exchange works by agreeing on two publicly shared values: a large prime number $q$ and a primitive root $g$. Alice and Bob each generate a secret key—a large random number—$x_a$ and $x_b$ respectively, and each raise the primitive root to the power of the secret key, modulo the large prime number.
$$
\begin{align*}
y_a &= g^{x_a} \bmod q \\
y_b &= g^{x_b} \bmod q
\end{align*}
$$
The results are sent to each other and the shared key is computed by raising the received value to the secret key modulo the primitive root.
$$
\begin{align*}
k_{ab} &= y_b^{x_a} \bmod q \\
k_{ab} &= y_a^{x_b} \bmod q
\end{align*}
$$
Given a prime number $q$, a primitive root $g$ is a number such that every number from 1 up to $q - 1$ can be computed by raising the primitive root to some number $k$.
$$
\forall x \in \{1, 2, ..., q - 1\}\ \mathbb{Z}_q \\
\exists k \text { such that } g^k = x
$$
A common analogy is that of mixing paint.